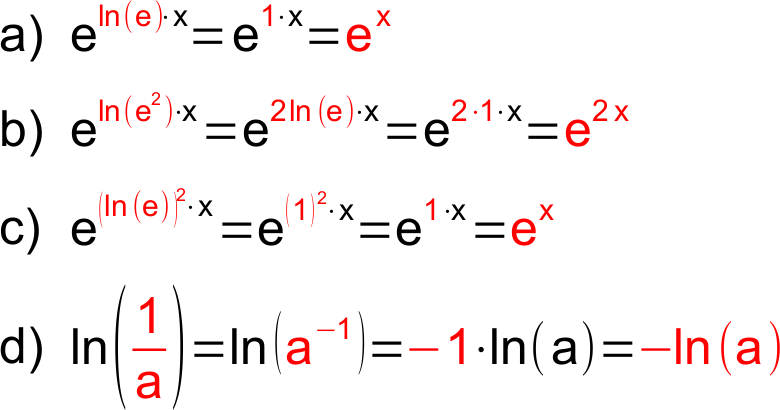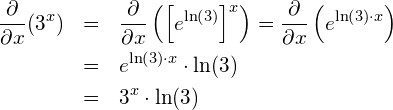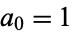Factorial exponencial

El factorial exponencial es un entero positivo n elevado a la potencia n-1, el cual a su vez está elevada a la potencia n-2, y así sucesivamente. Se suele usar como notación el símbolo identificativo del factorial en el lugar del exponente ${\displaystyle n^{!}}$. Se define:^[1]​^[2]​

${\displaystyle a_{n}=n^{\left(n-1\right)^{\left(n-2\right)^{\cdots }}}\,}$

También puede definirse mediante la siguiente relación de recurrencia:^[2]​

${\displaystyle a_{0}=1,\quad a_{n}=n^{a_{n-1}}\,}$

Los primeros factoriales exponenciales son:^[2]​

Su crecimiento es mayor que el de los factoriales e incluso que el de los hiperfactoriales. El factorial exponencial de n=5 tiene 183.231 dígitos.^[1]​^[2]​

La suma infinita de los inversos de los factoriales exponenciales es:

${\displaystyle S=\sum _{k=1}^{\infty }{\frac {1}{a_{k}}}={\frac {1}{1}} {\frac {1}{2}} {\frac {1}{9}} {\frac {1}{262144}} \cdots =1,6111149258083767361111\ldots }$

cuyo resultado es un número de Liouville, y por tanto irracional.^[3]​

Referencias

Enlaces externos

• Very Big Number, Nrich (1999) (en inglés)